Dynamic Importance Sampling and Beyond
Negative learning rates help escape local traps.
Point estimation tends to over-predict out-of-distribution samples (Lakshminarayanan et al., 2017) and leads to unreliable predictions. Given a cat-dog classifier, can we predict flamingo as the unknown class?

The key to answering this question is uncertainty, which is still an open question. Yarin gave a good tutorial on uncertainty predictions using Dropout (Gal, n.d.). However, that method tends to underestimate uncertainty due to the nature of variational inference.
Importance sampling
How can we give efficient uncertainty quantification for deep neural networks? To answer this question, we first show a baby example. Suppose we are interested in a Gaussian mixture distribution, the standard stochastic gradient Langevin dynamics (Welling & Teh, 2011) suffers from the local trap issue.
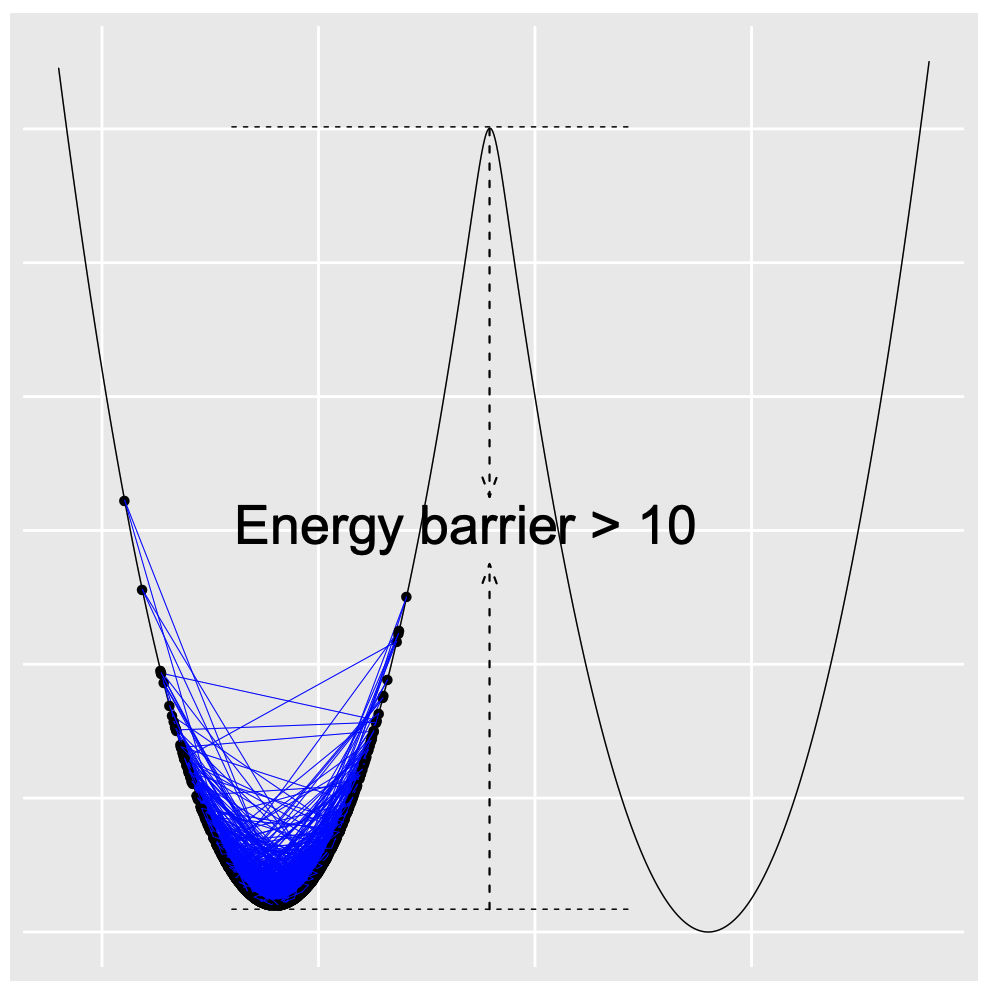
To tackle that issue and accelerate computations, we consider importance sampling
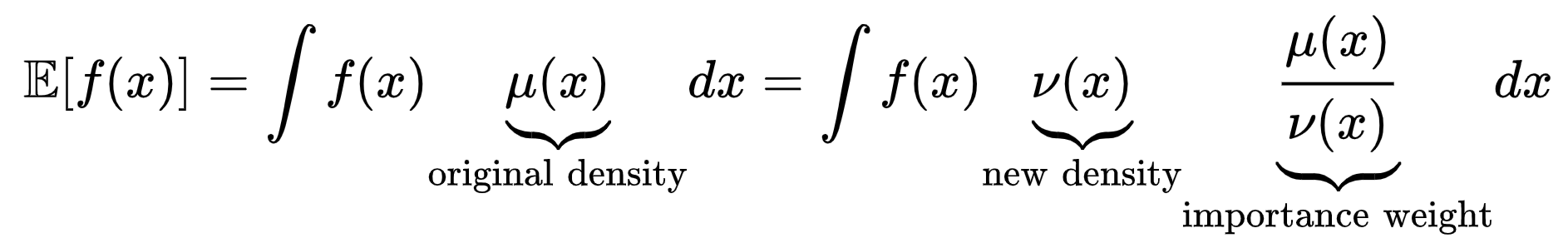
That is when the original density is hard to simulate, but the new density is easier. Together with the importance weight, we can obtain an estimate indirectly by sampling from a new density.
Build a flattened density
What kind of distribution is easier than the original? A flattened distribution!
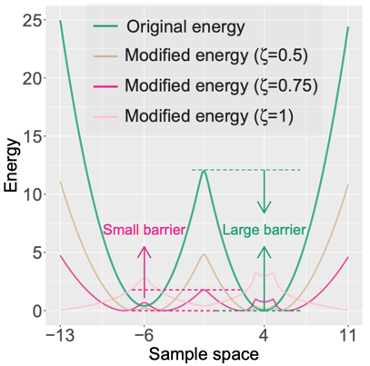
How to build such a flat density? One famous example is annealed importance sampling via high temperatures; another (ours) is to exploit ideas from Wang-Landau algorithm and divide the original density by the energy PDF.
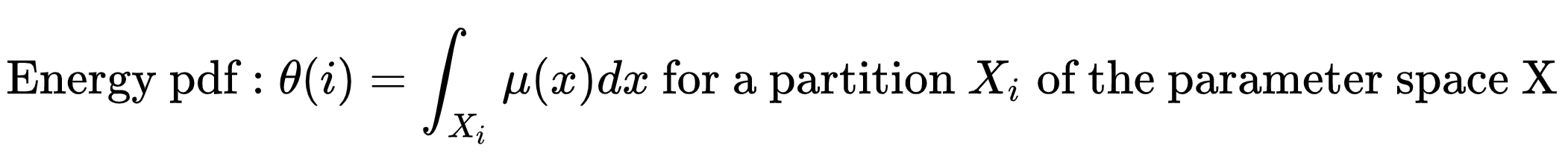
Given the energy PDF, we can enjoy a random walk in the energy space. Moreover, the bias caused by simulating from a different density can be adjusted by the importance weight.
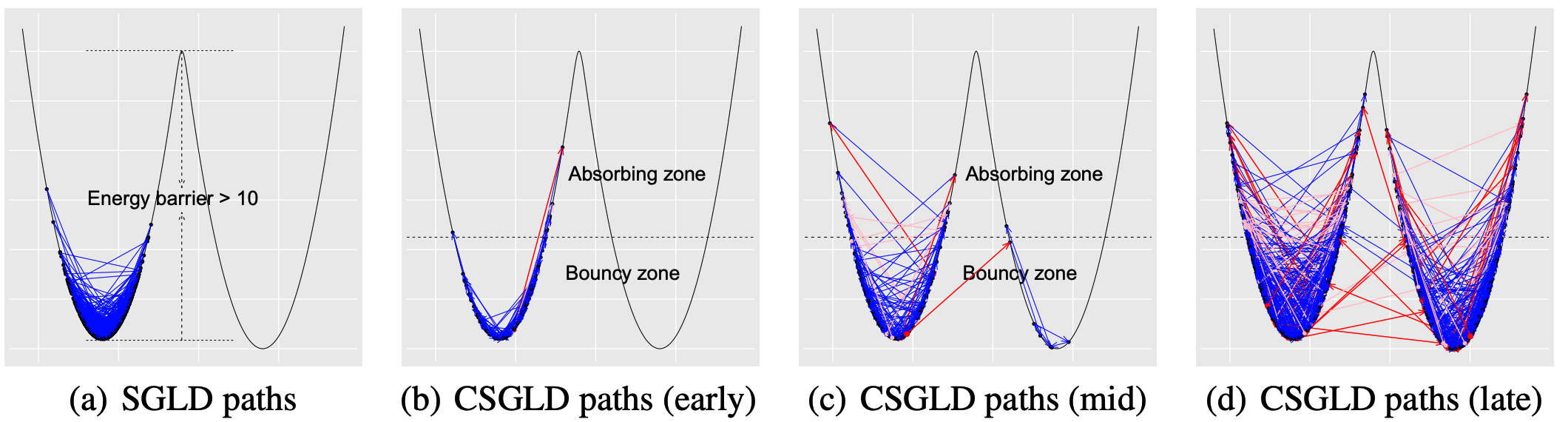
Sample trajectory in terms of learning rates
CSGLD possesses a self-adjusting mechanism to escape local traps. Most notably, it leads to smaller or even negative learning rates in low energy regions to bounce particles out.
Estimate the energy PDF via stochastic approximation
Since we don’t know the energy PDF in the beginning, we can adaptively estimate it on the fly via stochastic approximation. In the long run, we expect that the energy PDF is gradually estimated and we can eventually simulate from the target flat density. Theoretically, this algorithm has a stability property such that the estimate of energy PDF converges to a unique fixed point regardless of the non-convexity of the energy function.
The following is a demo to show how the energy PDF is estimated. In the beginning, CSGLD behaves similarly to SGLD. But soon enough, it moves quite freely in the energy space.


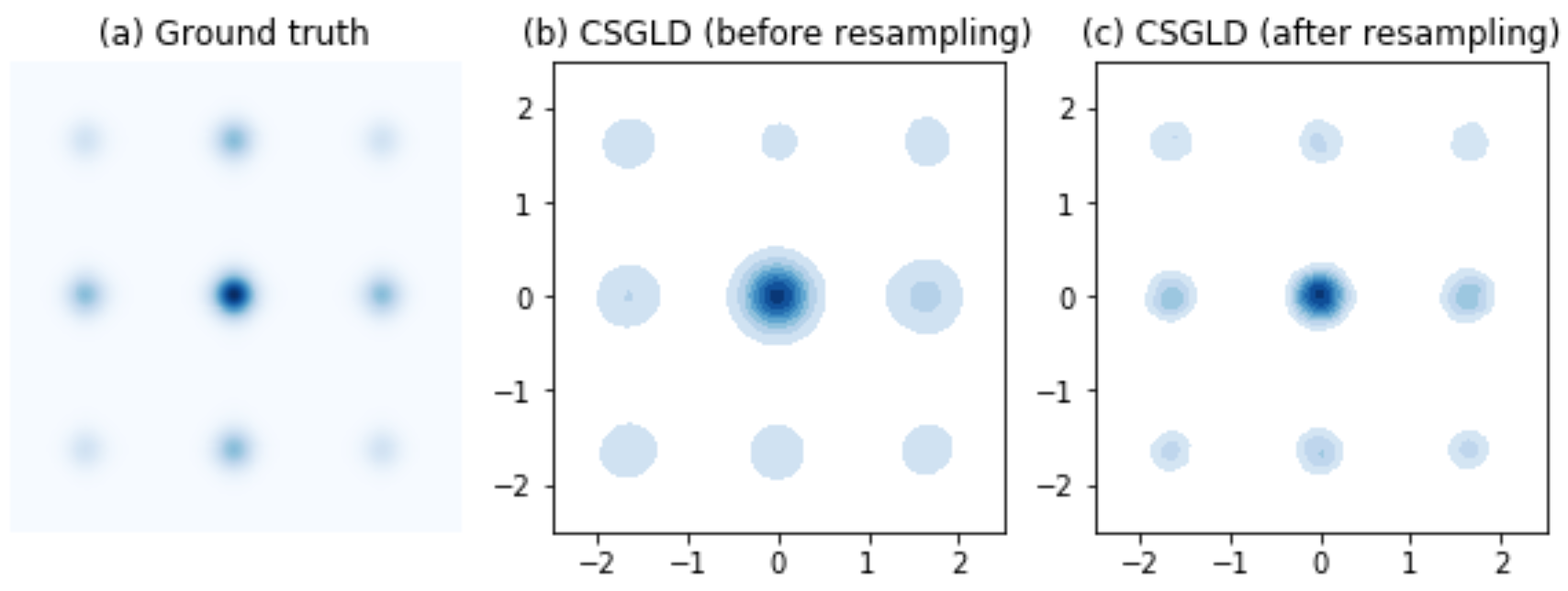
The following result shows [code] what the flattened and reweighted densities look like.
Comparison with other methods
We compare CSGLD (Deng et al., 2020) with SGLD (Welling & Teh, 2011), (Zhang et al., 2020), and (Deng et al., 2020), and observe that CSGLD is comparable to reSGLD and faster than SGLD and cycSGLD.

| Methods | Special features | Cost |
|---|---|---|
| SGLD (ICML’11) | None | None |
| Cycic SGLD (ICLR’20) | Cyclic learning rates | More cycles |
| Replica exchange SGLD (ICML’20) | Swaps/Jumps | Parallel chains |
| Contour SGLD (NeurIPS’20) | Bouncy moves | Latent vector |
Summary
Contour SGLD can be viewed as a scalable Wang-Landau algorithm in deep learning. It paves the way for future research in various adaptive biasing force techniques for big data problems. We are working on extensions of this algorithm in both theory and large-scale AI applications. If you like this paper, you can cite
@inproceedings{CSGLD,
title={A Contour Stochastic Gradient Langevin Dynamics Algorithm for Simulations of Multi-modal Distributions},
author={Wei Deng and Guang Lin and Faming Liang},
booktitle={Advances in Neural Information Processing Systems},
year={2020}
}
For Chinese readers, you may also find this blog interesting 知乎.
- Lakshminarayanan, B., Pritzel, A., & Blundell, C. (2017). Simple and Scalable Predictive Uncertainty Estimation using Deep Ensemble. NeurIPS.
- Gal, Y. What My Deep Model Doesn’t Know... Blog.
- Welling, M., & Teh, Y. W. (2011). Bayesian Learning via Stochastic Gradient Langevin Dynamics. ICML.
- Deng, W., Lin, G., & Liang, F. (2020). A Contour Stochastic Gradient Langevin Dynamics Algorithm for Simulations of Multi-modal Distributions. Neurips.
- Zhang, R., Li, C., Zhang, J., Chen, C., & Wilson, A. G. (2020). Cyclical Stochastic Gradient MCMC for Bayesian Deep Learning. ICLR.
- Deng, W., Feng, Q., Gao, L., Liang, F., & Lin, G. (2020). Non-Convex Learning via Replica Exchange Stochastic Gradient MCMC. ICML.